📚 1/6
📚 量子コンピューティング入門
量子コンピュータ入門 #1：量子コンピュータのための数学基礎
量子コンピュータを深く理解するために不可欠な数学的道具（複素数、ベクトル、行列、テンソル積）と、物理学特有の表記法である「ブラケット記法」を、大学1〜2年生向けに厳密かつ直感的に解説します。
量子コンピュータ数学線形代数
by 中田拓海読む
サイエンス
自然科学・数理科学・計算科学の最先端研究
6件の記事
タグ:
📚 2/6
📚 量子コンピューティング入門
量子コンピュータ入門 #2：情報のベクトル表現と量子ビット
量子コンピュータを「魔法の箱」としてではなく、「線形代数で記述される物理系」として理解します。情報のベクトル表現、量子ビットの数学的定義、そして測定の原理を解説します。
量子コンピュータ量子力学線形代数
by 中田拓海読む
📚 3/6
📚 量子コンピューティング入門
量子コンピュータ入門 #3：ブロッホ球と量子ゲートのユニタリ性
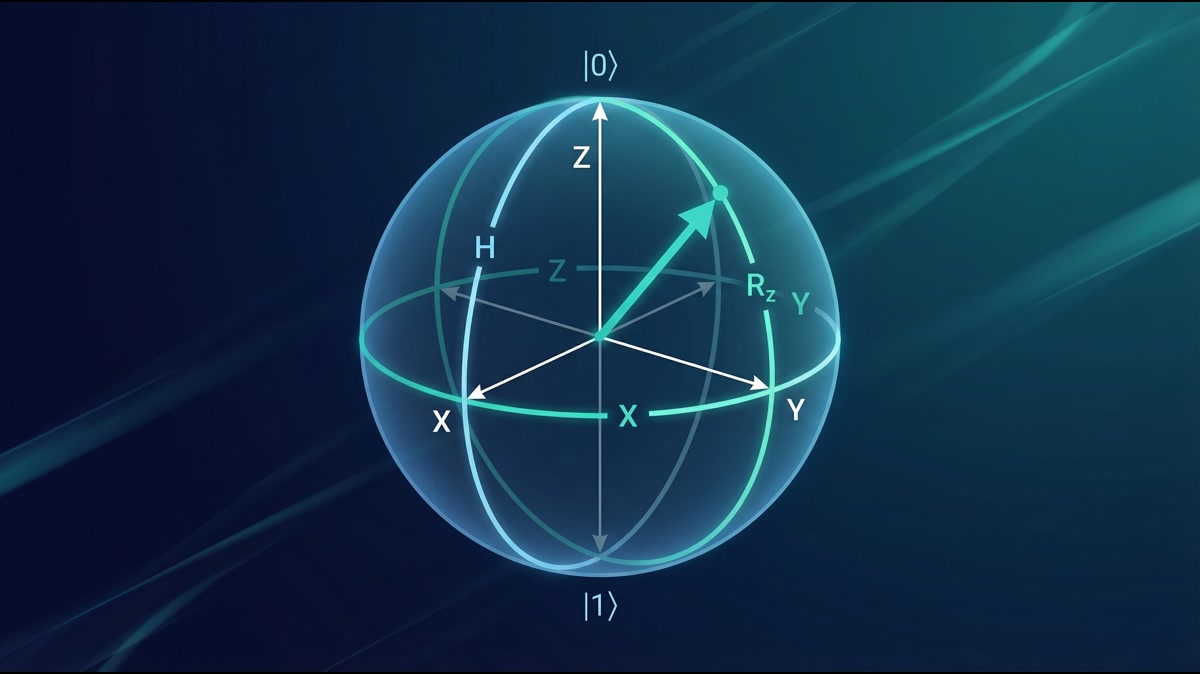
量子ビットの幾何学的表現である「ブロッホ球」を数式から導出します。また、量子ゲートがなぜ「ユニタリ行列」でなければならないのか、その数学的理由と物理的意味を解説します。
量子ビットブロッホ球ユニタリ行列
by 中田拓海読む
📚 4/6
📚 量子コンピューティング入門
量子コンピュータ入門 #4：テンソル積とエンタングルメント
「量子もつれ」はSFではありません。テンソル積を用いて多量子ビット系を記述し、エンタングルメントを「因数分解不可能性」として数学的に定義・証明します。
量子もつれエンタングルメントテンソル積
by 中田拓海読む
📚 5/6
📚 量子コンピューティング入門
量子コンピュータ入門 #5：量子アルゴリズムの仕組み（ドイチュ・ジョサとグローバー）
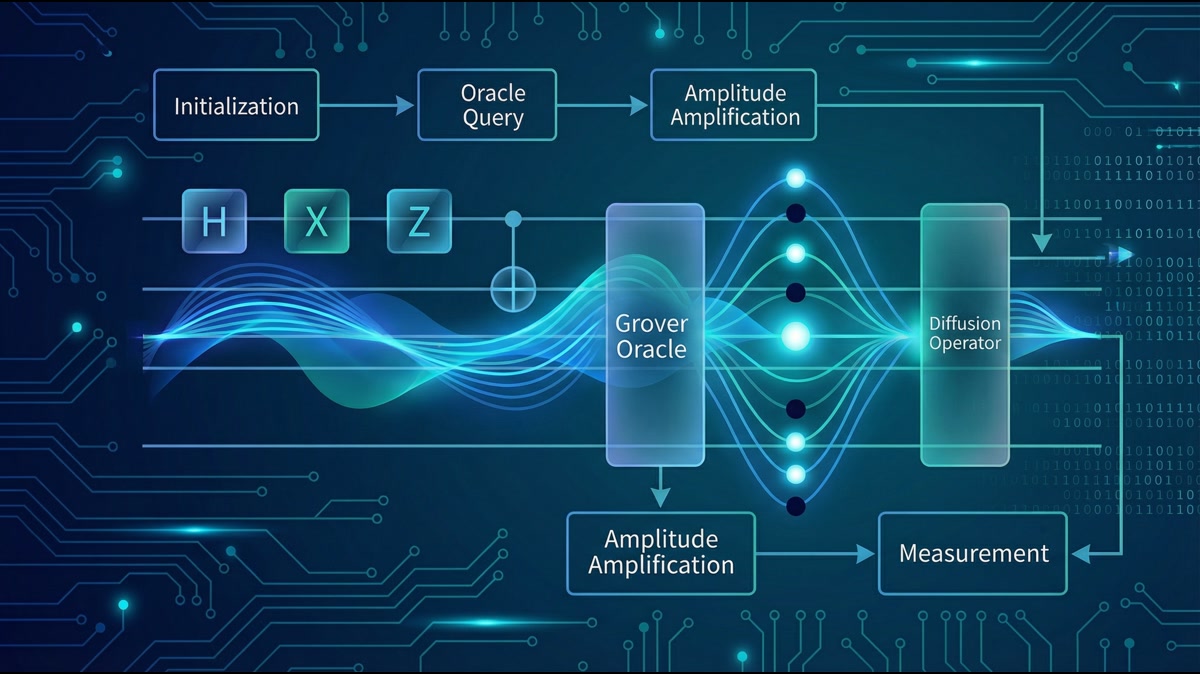
量子コンピュータはなぜ速いのか？その秘密は「量子干渉」にあります。最も単純なドイチュのアルゴリズムと、探索を行うグローバーのアルゴリズムを数式で追いながら、そのメカニズムを解明します。
量子アルゴリズムドイチュ・ジョサグローバーのアルゴリズム
by 中田拓海読む
📚 6/6
📚 量子コンピューティング入門
量子コンピュータ入門 #6：ショアのアルゴリズムと量子フーリエ変換
現代暗号を破壊する可能性を持つ「ショアのアルゴリズム」。その数学的構造である「位数発見問題」への帰着と、周期性を抽出する「量子フーリエ変換」の魔術を解説します。
ショアのアルゴリズムRSA暗号量子フーリエ変換
by 中田拓海読む