量子コンピュータ入門 #3：ブロッホ球と量子ゲートのユニタリ性

前回は、量子ビットが複素ベクトル $|\psi\rangle = \alpha|0\rangle + \beta|1\rangle$ で表されることを学びました。 今回は、この抽象的な複素ベクトルを、私たちが直感的に理解できる3次元空間上の「回転」として視覚化する ブロッホ球（Bloch Sphere） の概念を導きます。

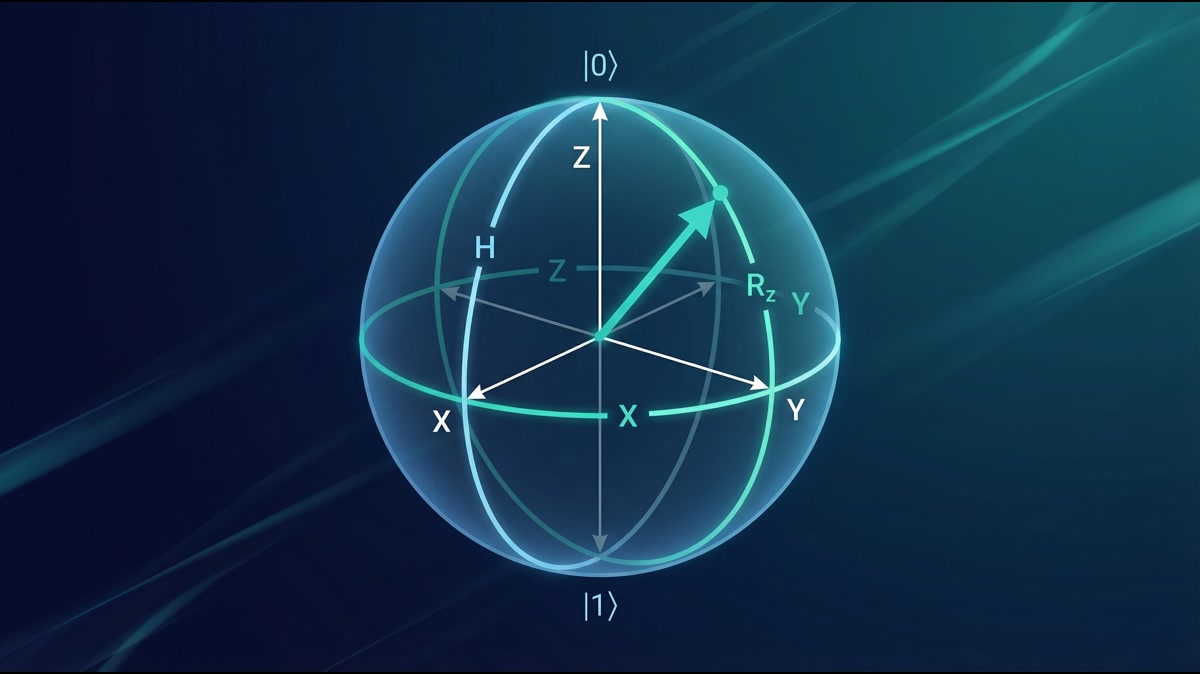
1. ブロッホ球の導出

2つの複素数 $\alpha, \beta$ で表される量子状態を、より少ないパラメータで表現できないか考えます。

自由度の削減

初期状態の自由度は、実部と虚部で計4つの実数パラメータがあります。

1. 正規化条件: $|\alpha|^2 + |\beta|^2 = 1$ という制約があるため、自由度は3つに減ります。
2. グローバル位相の無視: $|\psi\rangle$ と $e^{i\gamma}|\psi\rangle$ は物理的に区別できないため、全体の位相 $\gamma$ を無視できます。これで自由度は2つになります。

極座標表示

まず、$\alpha, \beta$ を極形式で書きます。

$\alpha = r_\alpha e^{i\phi_\alpha}, \quad \beta = r_\beta e^{i\phi_\beta}$

グローバル位相 $e^{i\phi_\alpha}$ をくくり出します。

$|\psi\rangle = e^{i\phi_\alpha} (r_\alpha |0\rangle + r_\beta e^{i(\phi_\beta - \phi_\alpha)} |1\rangle)$

グローバル位相 $e^{i\phi_\alpha}$ を無視し、相対位相を $\phi = \phi_\beta - \phi_\alpha$ と置きます。さらに、正規化条件 $r_\alpha^2 + r_\beta^2 = 1$ を満たすように、三角関数を用いて $r_\alpha = \cos(\theta/2), r_\beta = \sin(\theta/2)$ と置くことができます（$0 \le \theta \le \pi$）。

こうして、量子ビットの一般形が得られます：

$|\psi\rangle = \cos\frac{\theta}{2}|0\rangle + e^{i\phi}\sin\frac{\theta}{2}|1\rangle$

ここで、変数 $\theta$ と $\phi$ は以下の範囲を取ります。

• $0 \le \theta \le \pi$ （極角）
• $0 \le \phi < 2\pi$ （方位角）

これはまさに、3次元単位球面の球面座標系に対応します。この球を ブロッホ球 と呼びます。

なぜ $\theta/2$ なのか？

「なぜ $\theta$ ではなく $\theta/2$ なのか？」という疑問は、ベクトル空間とブロッホ球の対応関係における最大のポイントです。

ベクトル空間において、$|0\rangle$ と $|1\rangle$ は 直交 しています（角度 $90^\circ$）。 一方、ブロッホ球上では、$|0\rangle$（北極、$\theta=0$）と $|1\rangle$（南極、$\theta=\pi$）は 反対側 に位置しています（角度 $180^\circ$）。

ベクトル空間での角度を2倍したものが、ブロッホ球上の角度になります。これにより、直交する状態が球面上では正反対の位置に対応し、幾何学的な直感が働きやすくなります。

2. 量子ゲートとユニタリ行列

量子ビットの状態を変える操作（量子ゲート）は、ベクトルに対する線形変換、つまり行列 $U$ で表されます。 $|\psi'\rangle = U|\psi\rangle$

ユニタリ性の要請

量子力学では、時間発展（状態変化）において「全確率が1である」という事実は変わりません。つまり、ベクトルの長さ（ノルム）が保存される必要があります。

$\langle \psi' | \psi' \rangle = \langle \psi | U^\dagger U | \psi \rangle = \langle \psi | \psi \rangle = 1$

これが任意の $|\psi\rangle$ で成り立つためには、以下が必要です。

$U^\dagger U = I$

このような性質を持つ行列を ユニタリ行列 と呼びます。 幾何学的には、ユニタリ変換は複素ベクトル空間における「回転」に対応します。

3. 基本的な1量子ビットゲート

代表的な量子ゲートを行列とブロッホ球上の回転として見てみましょう。

パウリ行列（X, Y, Z）

パウリ行列は、ブロッホ球の $x, y, z$ 軸周りの $180^\circ$ 回転（$\pi$ 回転）に対応します。

Xゲート（ビット反転）

$X = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}$ $|0\rangle \leftrightarrow |1\rangle$ を入れ替えます。ブロッホ球ではX軸周りに180度回転させ、北極を南極へ移動させます。

Zゲート（位相変転）

$Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$ $|1\rangle$ の位相だけを反転させます（$\alpha|0\rangle + \beta|1\rangle \to \alpha|0\rangle - \beta|1\rangle$）。 ブロッホ球ではZ軸周りの回転に対応し、北極・南極の位置は変えず、赤道上の位相 $\phi$ を回転させます。

アダマールゲート（H）

重ね合わせ状態を作る最も重要なゲートです。

$H = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}$

計算例：$|0\rangle$ への作用

$H|0\rangle = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 \\ 1 \end{pmatrix} = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) = |+\rangle$

これはブロッホ球の $x$ 軸上の点（$\theta=\pi/2, \phi=0$）に対応します。 幾何学的には、Hゲートは「X軸とZ軸の中間の軸」周りの180度回転と解釈できます。

一般的な回転ゲート

任意の軸 $\vec{n} = (n_x, n_y, n_z)$ 周りの角度 $\Theta$ の回転は、パウリ行列を用いて以下のように書けます（ここでも $\Theta/2$ が現れることに注意）。

$R_{\vec{n}}(\Theta) = \exp(-i \frac{\Theta}{2} \vec{n} \cdot \vec{\sigma}) = I \cos\frac{\Theta}{2} - i(\vec{n} \cdot \vec{\sigma})\sin\frac{\Theta}{2}$

ここで $\vec{\sigma} = (X, Y, Z)$ です。この式はオイラーの公式の行列表現と言えます。

まとめ

• ブロッホ球: 量子ビットの状態空間 $\mathbb{C}^2$ を3次元球面 $\mathbb{S}^2$ に写像したもの。
• $\theta/2$ の魔法: ベクトル空間での直交関係が、球面上での対蹠点（反対側）に対応する。
• ユニタリ性: 量子ゲートは確率の総和を保存するため、ユニタリ行列でなければならない。
• ゲート操作: 量子ゲートの適用は、ブロッホ球上での回転操作と等価である。

次回は、量子ビットを2つに増やし、量子力学の最も不思議な性質である「エンタングルメント（量子もつれ）」をテンソル積を用いて記述します。

次へ：量子コンピュータ入門 #4：テンソル積とエンタングルメント

参考資料

• Preskill, J. (2018). Quantum Computing in the NISQ era and beyond.
• IBM Quantum Learning: https://learning.quantum.ibm.com/
• Qiskit Textbook: https://qiskit.org/learn

更新履歴

ご注意: 本記事は2025年12月時点の情報に基づいています。最新情報は公式サイトをご確認ください。