量子コンピュータ入門 #5：量子アルゴリズムの仕組み（ドイチュ・ジョサとグローバー）

量子ビットとゲートが揃いました。いよいよ、これらを使って「古典コンピュータより速く」問題を解く方法、すなわち量子アルゴリズムを解説します。 キーワードは 量子並列性（Quantum Parallelism） と干渉（Interference） です。

1. 量子並列性とオラクル

全状態の同時生成

$n$ 個の量子ビットをすべて $|0\rangle$ に初期化し、それぞれにアダマールゲート $H$ を適用します。

$|\psi_0\rangle = H^{\otimes n} |0\rangle^{\otimes n} = \left(\frac{|0\rangle + |1\rangle}{\sqrt{2}}\right)^{\otimes n} = \frac{1}{\sqrt{2^n}} \sum_{x=0}^{2^n-1} |x\rangle$

たった1ステップで、$0$ から $2^n-1$ までのすべての整数の重ね合わせ状態を作ることができます。これが量子並列性の基礎です。

量子オラクル（Oracle）

ある関数 $f(x)$ （出力は0か1）を計算するブラックボックス（オラクル）を考えます。量子回路では、可逆性を保つために以下のようなユニタリ変換 $U_f$ として定義します。

$U_f |x\rangle |y\rangle = |x\rangle |y \oplus f(x)\rangle$

ここで $\oplus$ は排他的論理和（XOR）です。

位相キックバック（Phase Kickback）

ここが重要なテクニックです。第2レジスタ（$|y\rangle$）を $|-\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)$ に設定して $U_f$ を作用させてみましょう。

$U_f |x\rangle |-\rangle = |x\rangle \frac{1}{\sqrt{2}}(|0 \oplus f(x)\rangle - |1 \oplus f(x)\rangle)$

• $f(x)=0$ のとき：$|x\rangle \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle) = |x\rangle |-\rangle$
• $f(x)=1$ のとき：$|x\rangle \frac{1}{\sqrt{2}}(|1\rangle - |0\rangle) = -|x\rangle |-\rangle$

まとめると： $U_f |x\rangle |-\rangle = (-1)^{f(x)} |x\rangle |-\rangle$

第2レジスタは変化せず、関数 $f(x)$ の値が 位相（符号）として第1レジスタに「キックバック」 されました。これにより、関数の情報を位相に埋め込むことができます。

2. ドイチュのアルゴリズム

最も単純な例として、ドイチュのアルゴリズム（Deutsch's Algorithm）を解きます。

問題設定

入力 $x \in \{0, 1\}$、出力 $f(x) \in \{0, 1\}$ の関数 $f$ が与えられます。 関数は以下の2種類のどちらかです。

1. 定数関数 (Constant): $f(0) = f(1)$ （両方0、または両方1）
2. バランス関数 (Balanced): $f(0) \neq f(1)$ （片方が0、もう片方が1）

古典コンピュータでは、$f(0)$ と $f(1)$ の2回計算しないと判別できません。量子コンピュータなら 1回 で判別できます。

アルゴリズムの手順

1. 初期状態：$|0\rangle |1\rangle$

2. 両方にHゲート：$|+\rangle |-\rangle$

3. オラクル $U_f$ 適用（位相キックバック）： $|\psi_2\rangle = \frac{1}{\sqrt{2}} \sum_{x=0}^1 (-1)^{f(x)} |x\rangle \otimes |-\rangle$

   第1レジスタだけ見ると： $\frac{1}{\sqrt{2}} ((-1)^{f(0)}|0\rangle + (-1)^{f(1)}|1\rangle)$

4. 第1レジスタに再びHゲートを適用： $H|0\rangle = |+\rangle, \quad H|1\rangle = |-\rangle$

   $|\psi_3\rangle = \frac{1}{2} [(-1)^{f(0)}(|0\rangle + |1\rangle) + (-1)^{f(1)}(|0\rangle - |1\rangle)]$

   これを整理すると（$|0\rangle$ と $|1\rangle$ の係数をまとめる）： $= \frac{1}{2} [((-1)^{f(0)} + (-1)^{f(1)})|0\rangle + ((-1)^{f(0)} - (-1)^{f(1)})|1\rangle]$

結果の解析

• 定数関数の場合 ($f(0)=f(1)$):

  • $|0\rangle$ の係数：$\pm (1+1)/2 = \pm 1$
  • $|1\rangle$ の係数：$\pm (1-1)/2 = 0$
  • $\Rightarrow$ 測定結果は必ず 0

• バランス関数の場合 ($f(0) \neq f(1)$):

  • $|0\rangle$ の係数：$\pm (1-1)/2 = 0$
  • $|1\rangle$ の係数：$\pm (1-(-1))/2 = \pm 1$
  • $\Rightarrow$ 測定結果は必ず 1

このように、干渉 によって正解の確率振幅を強め合い、不正解を打ち消し合うことで、1回の計算で関数の性質を決定できました。

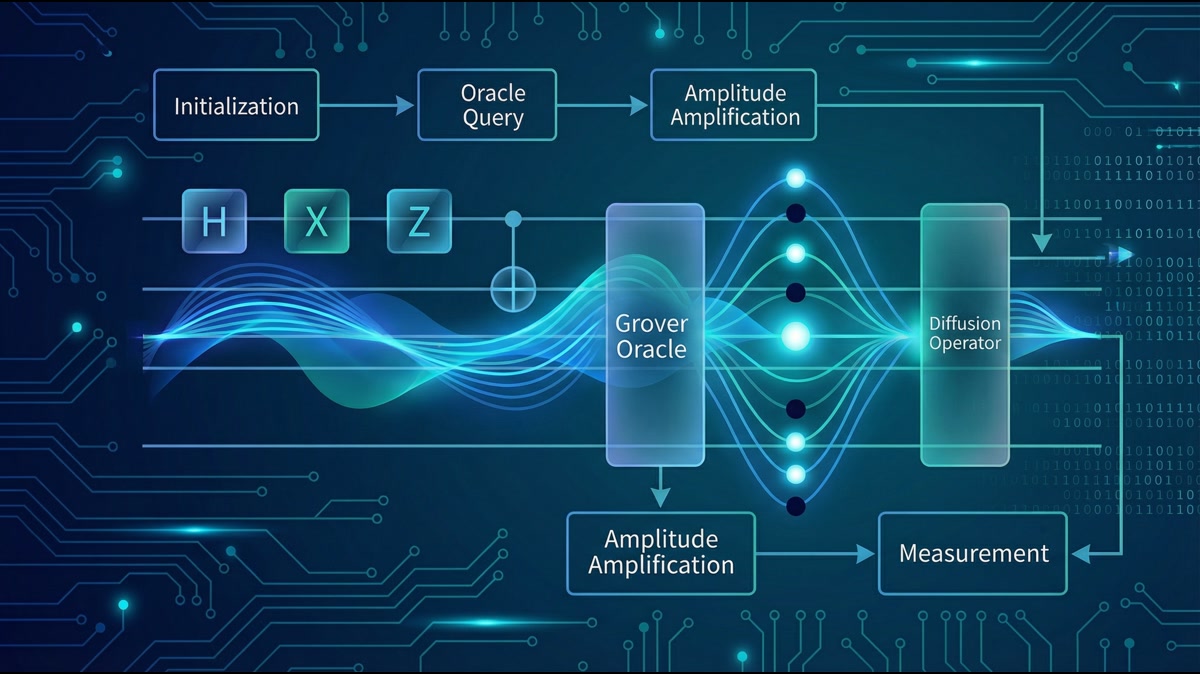
3. グローバーのアルゴリズム

これを拡張し、データ探索を行うのがグローバーのアルゴリズムです。 $N=2^n$ 個のデータから、条件 $f(w)=1$ を満たす解 $w$ を探します。

幾何学的解釈

状態空間を「正解 $|w\rangle$」と「それ以外 $|s^\perp\rangle$」の2次元平面で考えます。

初期状態 $|s\rangle$（全探索空間の重ね合わせ）は、ほとんど $|s^\perp\rangle$ に近く、ほんの少しだけ $|w\rangle$ 成分を含んでいます。

$|s\rangle = \sin\theta |w\rangle + \cos\theta |s^\perp\rangle$

ここで $\sin\theta = 1/\sqrt{N}$ です。

グローバー反復

1. オラクル $U_f$: 正解 $|w\rangle$ の符号を反転します（位相キックバック）。 幾何学的には、$|s^\perp\rangle$ 軸に対する鏡映反転です。

2. 拡散演算子 $D$: 初期状態 $|s\rangle$ 周りの反転を行います。 $D = 2|s\rangle\langle s| - I$ 幾何学的には、ベクトル $|s\rangle$ に対する鏡映反転です。

この2つの鏡映操作を組み合わせると、状態ベクトルは平面上で $2\theta$ だけ回転します。これを繰り返すことで、状態ベクトルを $|w\rangle$ に近づけます。

計算量

1回の反復で角度が $2\theta \approx 2/\sqrt{N}$ 進みます。 $|w\rangle$（角度 $\pi/2$）に到達するには、およそ以下の回数が必要です。

$k \approx \frac{\pi/2}{2/\sqrt{N}} \approx \frac{\pi}{4}\sqrt{N}$

古典探索の $O(N)$ に対し、$O(\sqrt{N})$ の二乗加速を実現します。

まとめ

• 量子並列性: 全状態の重ね合わせに対して一度に関数を適用できる。
• 位相キックバック: 関数の値を位相情報に変換する重要テクニック。
• 量子干渉: 確率振幅の足し合わせ（強め合い・打ち消し合い）を利用して、欲しい答えの確率を高める。
• グローバーのアルゴリズム: 振幅増幅を用いて、確率的に解を探索する。

次回は、現代の暗号システムを脅かす「ショアのアルゴリズム」について、その核心である「量子フーリエ変換」と「周期発見」の仕組みを解説します。

次へ：量子コンピュータ入門 #6：ショアのアルゴリズムと量子フーリエ変換

参考資料

• Shor, P. W. (1994). Algorithms for quantum computation.
• Grover, L. K. (1996). A fast quantum mechanical algorithm for database search.
• Quantum Algorithm Zoo: https://quantumalgorithmzoo.org/

更新履歴

ご注意: 本記事は2025年12月時点の情報に基づいています。最新情報は公式サイトをご確認ください。